When building machine learning and artificial intelligence models you’ll often run into situations where a model is not working as well as you would like. Maybe the error rate is too high or the model works fine on the training data, but fails when you apply real world data.

What should you do to improve it: get more training data? create a more complex model? tweak you model parameters? there are many avenues to consider, and one can easily waste a ton of time exploring each of them.

This blog posts will walk you through how to systematically approach debugging and diagnosing your machine learning algorithm to make an informed decision about how to improve it.

Typical problems

A machine learning algorithm will generally suffer from one of two problems – high bias or high variance.

• High bias is when your algorithm is bad at fitting the data and miss relevant relations between the input features and the predicted output. High bias is also called underfitted – meaning your model is not fitting the data very well and makes poor predictions.
• High variance on the other hand is when your algorithm is bad at generalizing. This is normally the case if your algorithm fit the training data perfectly, but when applied to previously unseen data it fails to make good predictions. High variance is also called overfitting.

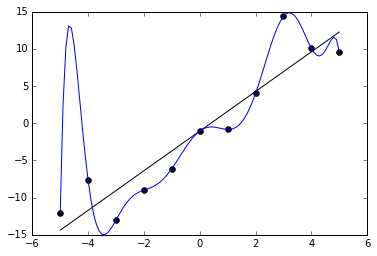
The image below shows examples of a model with high bias (black line) and with high variance (blue line).

This blog post will help you understand if your model is suffering from high bias or high variance and give you some ideas how to improve it, but first we must get some definitions down.

Setting the scene

In order to apply this blog post to your machine learning problem you must know how to calculate your generalization error and training error. Calculating the error rate for your machine learning algorithm, depends on the type of problem (i.e. is a regression problem or a classification problem) and which model you use (i.e.linear regression vs. logistic regression). However the terms generalization error and training error are always defined the same way. That is:

• the training error is the error rate of your model measured on the data you used to train your model
• the generalization error is the error rate of your model measured on previously unseen data for your model

To get these error rate you will divide your dataset into two. A training dataset and a test dataset. The split between the two are normally 70% of your data goes into your training data, and 30% into your test dataset. Before you split your dataset into two it is extremely important that you randomize your data. This will help to make sure that the training dataset and test dataset both contains samples over the entire spectrum of values you’re trying to predict.

The advantage of using a separate dataset for testing is that you will have a reference dataset that can be used to detect potential problems, and will help you make informed decisions about how to modify your model to make it even better.

Diagnosing the problem

With the two datasets in hand we are ready to diagnose our machine learning problem. To diagnose the problem we plot the learning curves of our model. To do so we calculate our training error and generalization error while varying the size of our training dataset (the test dataset must stay the same). Specifically we calculate the training error and generalization error when a training dataset has 1 data point up the maximum amount of data points in our training dataset.

Next we plot the two error rates in graph like this:

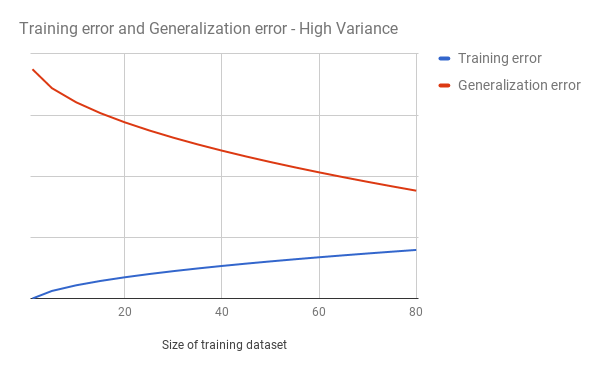
In this example we see that our training error (blue) slowly rises as we add more examples to our training dataset. This is expected since its normally easy for our algorithm to find a model that fits for a few examples, but harder to find an algorithm that works for many examples. We also see that our generalization error slow falls, but stays fairly high and never really converges with our training error.

This is a classic example of a model having high variance – that is our algorithm can approximate a solution for our training data, but not a general solution for our test data. To figure out how to improve an algorithm with high variance read the What’s next section below.

If on the other hand your plot looks something like this your algorithm may be suffering from high bias:

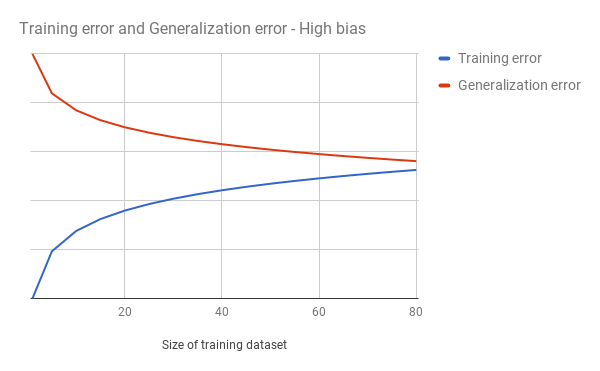
In this case our training error keeps rising rapidly when we increase the size of the training set. It is converging with our generalization error at a relatively high error rate. This is a typical indication of a high bias problem. Meaning that we are not able to properly capture relevant relations in our features in the model we have selected. If your model suffers from high bias read below for options to improve your algorithm.

It should be noted that the error curves are never as smooth as depicted above. If your curves have more bumps and noise its perfectly normal. 

What’s next?

At this point you should know if your model is suffering from high bias or high variance. Here are some suggestions for what you should be focusing on to improve your algorithm.

Improving a machine learning model suffering from high bias

To improve a model suffering from high bias you can do the following:

• Try getting additional features
  • The features you’re using for your algorithm may not contain enough information to make a solid prediction. Try getting more features to help your algorithm.
• Add complexity to your algorithm
  • Maybe your features need a little complexity to help capture the relevant information in your model.
  • Try adding polynomial terms for your numeric features (see Improving the accuracy section of Implementing Classification using Logistic Regression in Ruby for a practical example).
• Try decreasing λ when training your algorithm

Improving a machine learning model suffering from high variance

To improve a model suffering from high variance you can do the following:

• Get more training examples
  • More training examples may help your model find a better general solution
• Try a smaller set of features
  • Maybe you’re including too many features in your training set. Are there any features that can be removed?
• Try removing complexity from your features
  • Do you have polynomial terms in our feature matrix? maybe try to decrease the degree of the polynomial terms
• Try increasing λ when training your algorithm
  • If you want to know why read: How regularization can improve your machine learning algorithms